Recall from the introduction that the area of a $n$-side polygon with vertices $(x_1,y_1), (x_2,y_2), ... , (x_n,y_n)$ is $$A = \sum_{i=1}^{n} \frac{(x_{i+1}+x_i)(y_{i+1}-y_i)}{2} =\frac{1}{2} \sum_{i=1}^{n} \det\begin{pmatrix} x_i & x_{i+1} \\ y_i & y_{i+1} \end{pmatrix} $$ where $x_{n+1}:= x_1$, $y_{n+1}:=y_1$.
Interestingly, that is also the sum of determinants of the coordinates of vertices.
The formula of vector product[17], or cross product of two vectors $\mathbf{a}$ and $\mathbf{b}$ in 3D space is $$\mathbf{a} \times \mathbf{b} = |\mathbf{a}||\mathbf{b}| \sin{\theta} \ \mathbf{n},$$ where $\mathbf{n}$ is the unit vector perpendicular to the plane that contains $\mathbf{a}$ and $\mathbf{b}$, and $\theta$ is the angle between them in the plane.
Notice that the absolute value of norm of $\mathbf{a} \times \mathbf{b}$ is $||\mathbf{a} \times \mathbf{b}|| = |\mathbf{a}||\mathbf{b}| \sin{\theta}$, as $\mathbf{n}$ is the unit vector.
Also it can be written as the determinant. If $\mathbf{a} = a_1i + a_2j + a_3k$ and $\mathbf{b} = b_1i + b_2j+b_3k$, then $$\mathbf{a} \times \mathbf{b} = \left| {\begin{array}{*{20}{c}}{i}&{j}&{k}\\{{a_1}}&{{a_2}}&{{a_3}}\\{{b_1}}&{{b_2}}&{{b_3}}\end{array}} \right|.$$
If $\mathbf{a}$ and $\mathbf{b}$ are in 2D plane, i.e. $\mathbf{a} = a_1i + a_2j$ and $\mathbf{b} = b_1i + b_2j$, then $$\mathbf{a} \times \mathbf{b} = \left| {\begin{array}{*{20}{c}}{i}&{j}&{k}\\{{a_1}}&{{a_2}}&{{0}}\\{{b_1}}&{{b_2}}&{{0}}\end{array}} \right| = k\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|=(a_1b_2-a_2b_1)k,$$ which implies that $$| \mathbf{a} \times \mathbf{b}| = a_1b_2-a_2b_1.$$

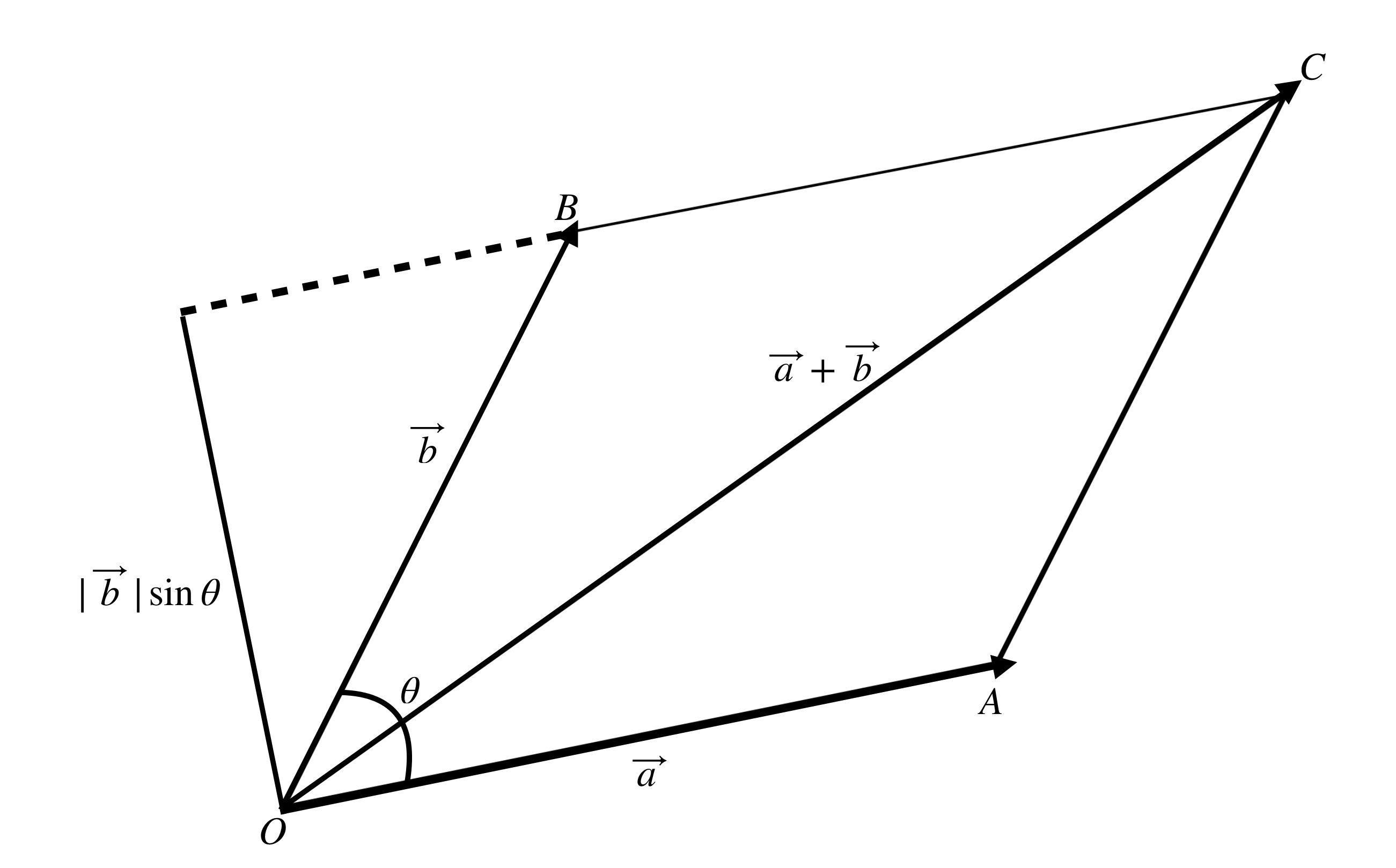
As shown in Figure 7.1, area $A$ of parallelogram formed by vectors $\mathbf{a}$ and $\mathbf{b}$ is $|\mathbf{a}||\mathbf{b}|\sin{\theta}$. Hence $$A = || \mathbf{a} \times \mathbf{b}|| = |\mathbf{a}||\mathbf{b}|\sin{\theta} = |a_1b_2-a_2b_1|,$$ which is also a determinant.
Similarly, area of triangle formed by two vectors can be found by the same method, just divide by 2.
© Group 18